Beer Pricing and Sizing: More Discounts and a Brief Pricing Primer
Hello again! This week we’re talking about discounts again (I had another thought on the topic), and finally, the basics of beer pricing, i.e. what constitutes a “correct” price in a simplistic sense
Discounts redux: partial discounts
So here’s another weird scenario. What happens if you sell Crowlers, but want to introduce a similar product, Growlers, at what amounts to a slight discount - if you originally sold 100% Crowlers, and by selling Growlers you get an x% boost above your base revenue, what % of Crowler sales can you “lose?” i.e. what is the break-even % of revenue that Crowlers comprise? (If you end up selling 100% Growlers at a discount, with no boost, you’ve lost money; if you sell 99% as many Crowlers but see a doubling of revenue, you’ve very likely made money; how do we attach an equation to this?)
First, let’s name the variables:
C = Crowler revenue
G = Growler revenue
b = % boost above 100% (base sales) - always taken as positive (otherwise we lose money)
d = % discount divided by margin
Why divide the discount % by margin? Stay tuned
Let’s begin with a pretty standard percentage equation: on the left hand side (LHS), we’ll put the new x% of Crowler revenue, the 100%+b%-x% of Growler revenue, and on the RHS we’ll put the original 100% Crowler revenue (why is b only applied to the Growlers? We’re assuming that selling them boosts overall revenue, and that we’re essentially cutting out a portion of Crowler revenue to give to the Growler revenue, on top of the boost - it’s the acceptable degree of this cannibalization that we’re trying to determine).
So:
x*C + (1+b-x)*G = 1*C = C
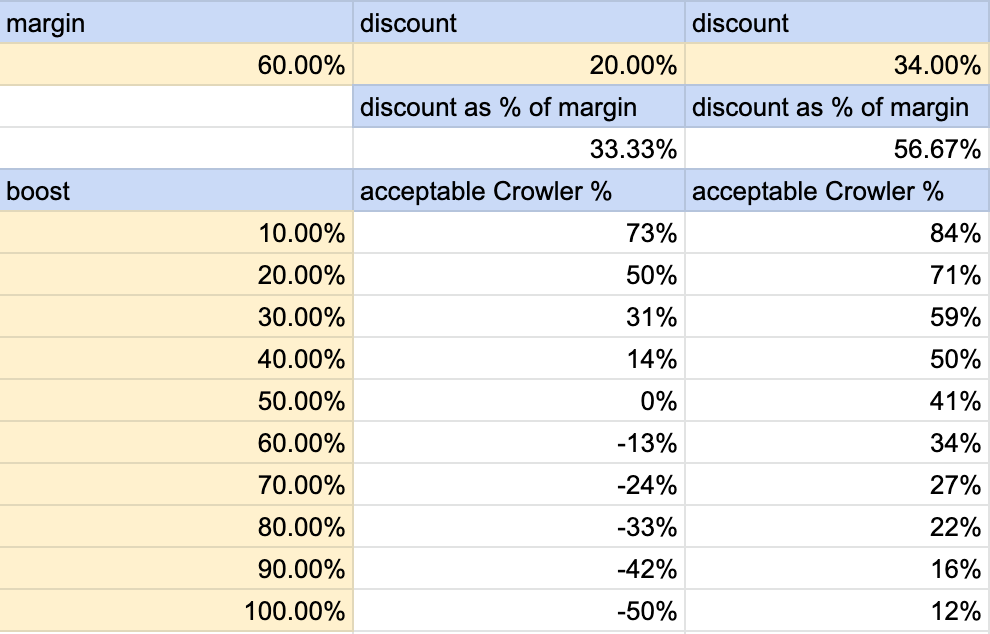
Immediately it behooves us to get G in terms of C. In our case, and this is particular to our business, our Crowlers are $14 (two are the same volume as a Growler, at $28), our Growlers are $22, and the jug is apparently $3.50, so our “real” revenue for Growlers is $18.50. Thus, our Growlers are effectively a ~34% discount on Crowlers. BUT, since we want to get the same profit and not just the same revenue, we must “normalize” this to our margin - if our margin is 60%, and we have a 60% discount, we make $0; further, if Growler profit (g) is g*m, Growler profit is also Crowler profit (c) minus the amount lost as a discount, or c*(m-d) = c*m - c*m*d/m. In other words, we can just use revenue and ignore margin in that equation above if we use a normalized discount instead of just the discount. So d mentioned above in the variables is actually 34%/60% ~ 57%. But I digress!
x*C + (1 + b - x)*G = x*C + (1 + b - x)*(1 - d)*C = C
Interestingly, C cancels out (good - this should be super general), and we get:
x + (1 + b - x)*(1 - d) = 1
x + (1 - d) + b*(1 - d) - x*(1 - d) = 1
x - x*(1 - d) = 1 - (1 - d) - b*(1 - d) = d - b*(1 - d)
x = (d - b*(1 - d))/(1 - (1 - d)) = (d - b*(1 - d))/d = 1 - b*(1 - d)/d = 1 - b/d + b
Cool! So this is the breakeven condition for x, the pct of Crowler sales you can afford to have vs your base revenue (100%). BUT, this is hardly the most useful form - we want to be able to just look up Crowler sales as a percentage of the total, not have to figure out what the “boost percentage” was - so we really want x/(1+b)
i.e.:
x/(1+b) = (1 - b/d + b)/(1+b) = 1 - (b/d)/(1+b)
Yikes! Kinda hairy, but very easy to crank out with a calculator. And does it make sense? (The physicist in me will always ask if it’s Gauge invariant)
if b is small relative to d, x is close to 100% - if your boost is small relative to your discount, you can’t afford to sell too many discounted items
as b->infinity, x/(1+b) -> 1-1/d = (d-1)/d, which I' don’t really get off of the bat - though since d ranges from 0%-100% (in this case, discount being equal to margin), the range is basically negative infinity to 0%…I think that’s because we’re trying to make the same profit with an infinite boost in revenue, so we have to “buy” a ton of Crowlers to make that work. Interesting. Not too useful though! Let’s not take b to infinity
In fact, here’s a spreadsheet!
So yeah! Pretty cool! I guess as we discussed above, a negative norm’d x means we make money no matter what (and I’m sure you could verify that using our previous discount/boost work)
Pricing: a brief primer
So, this is comically simple now - while the real fun stuff will have to wait until my econ class covers elasticity, we can make a quite simple claim:
if we charge $a for a pint, and our margin is m%, our profit per pint is a*m. If we want to consider charging $b for the pint, how many more/fewer pints could we sell before breaking even?
Assuming b>a, our profit on b is very interestingly not m*b - since our costs are identical, our new profit is b - a*(1-m), or b minus our original costs. Thus, to make the same amount of profit overall, we set
a*m*100% = (b - a*(1-m))*(100% - L), where L is basically a “negative boost percentage” (we take L as positive, though - think that’s tough? Thermodynamics will rip you to shreds)
so, solving for L,
a*m = b - a*(1-m) - L*(b - a*(1-m))
a*m - b + a - a*m = a - b = -L*(b - a + a*m)
L = (b - a)/(b - a + a*m)
So in the straightforward case where b - a = $1, L = 1/(1+a*m)
If margin is, again, 60%, and if a is $7, then L = 1/(1+7*.6) = 19%
So we can afford to lose 19% of our number of pints sold (right? Not pint revenue, right? I mean…our margin is now higher since our costs are a lower percentage…)
Similarly, if we charge a dollar less, or $6, we need a 19% boost in the number of pints sold, so the math doesn’t actually care about the direction of change, I just wanted you to see it in a straightforward way before generalizing it
And yeah, that’s a bunch of symbols - I’ll think of a visualization for the next post
See ya there!!